Norbert Wiener
| Norbert Wiener | |
|---|---|
 |
|
| Born | November 26, 1894 Columbia, Missouri, U.S. |
| Died | March 18, 1964 (aged 69) Stockholm, Sweden |
| Nationality | American |
| Fields | Mathematics Cybernetics |
| Institutions | Massachusetts Institute of Technology |
| Alma mater | Tufts College BA 1909 Harvard University PhD 1912 |
| Doctoral advisor | Karl Schmidt Josiah Royce |
| Doctoral students | Amar Bose Colin Cherry Shikao Ikehara Norman Levinson |
Norbert Wiener (November 26, 1894, Columbia, Missouri – March 18, 1964, Stockholm, Sweden) was an American mathematician.
A famous child prodigy, Wiener (pronounced WEE-nur) later became an early studier of stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.
Wiener is regarded as the originator of cybernetics, a formalization of the notion of feedback, with many implications for engineering, systems control, computer science, biology, philosophy, and the organization of society.
Contents |
Biography
Youth
Wiener was the first child of Leo Wiener and Bertha Kahn, both Ashkenazi Jews of Polish and German descent, respectively. Employing teaching methods of his own invention, Leo educated Norbert at home until 1903, except for a brief interlude when Norbert was 7 years of age. Wiener became a child prodigy partly due to his father's tutelage. Earning his living teaching German and Slavic languages, Leo read widely and accumulated a personal library from which the young Norbert benefited greatly. Leo also had ample ability in mathematics, and tutored his son in the subject until he left home.
After graduating from Ayer High School during 1906 at 11 years of age, Wiener entered Tufts College. He was awarded a BA for mathematics during 1909 at the age of 14, whereupon he began graduate studies of zoology at Harvard. During 1910 he transferred to Cornell to study philosophy.
Harvard
The next year he returned to Harvard, while still continuing his philosophical studies. Back at Harvard, Wiener became influenced by Edward Vermilye Huntington, whose mathematical interests ranged from axiomatic foundations to engineering problems. Harvard awarded Wiener a Ph.D. during 1912, when he was merely 18 years old, for a dissertation on mathematical logic, supervised by Karl Schmidt, the essential results of which were published as Wiener (1914). In that dissertation, he was the first to state publicly that ordered pairs can be defined in terms of elementary set theory. Hence relations can be defined by set theory, so that the theory of relations does not require any axioms or primitive notions distinct from those of set theory. During 1921, Kazimierz Kuratowski proposed a simplification of Wiener's definition of ordered pairs, and that simplification has been in common use ever since.
During 1914, Wiener traveled to Europe, to be taught by Bertrand Russell and G. H. Hardy at Cambridge University, and by David Hilbert and Edmund Landau at the University of Göttingen. During 1915-16, he taught philosophy at Harvard, then worked for General Electric and wrote for the Encyclopedia Americana. When World War I began, Oswald Veblen invited him to work on ballistics at the Aberdeen Proving Ground in Maryland. Thus Wiener, an eventual pacifist, wore a uniform during 1917-18. Living and working with other mathematicians strengthened his interest in mathematics.
After the war
After the war, Wiener was unable to secure a position at Harvard and was rejected for a position at the University of Melbourne. At W. F. Osgood's invitation, Wiener became an instructor of mathematics at MIT, where he spent the remainder of his career, becoming promoted eventually to Professor.
During 1926, Wiener returned to Europe as a Guggenheim scholar. He spent most of his time at Göttingen and with Hardy at Cambridge, working on Brownian motion, the Fourier integral, Dirichlet's problem, harmonic analysis, and the Tauberian theorems.
During 1926, Wiener's parents arranged his marriage to a German immigrant, Margaret Engemann; they had two daughters.
During and after World War II
During World War II, his work on the automatic aiming and firing of anti-aircraft guns caused Wiener to study communication theory and eventually to formulate cybernetics. After the war, his fame helped MIT to recruit a research team in cognitive science, composed of researchers in neuropsychology and the mathematics and biophysics of the nervous system, including Warren Sturgis McCulloch and Walter Pitts. These men later made pioneering contributions to computer science and artificial intelligence. Soon after the group was formed, Wiener ended all contact with its members, for reasons unknown.
Wiener later helped develop the theories of cybernetics, robotics, computer control, and automation. He shared his theories and findings with other researchers, and credited the contributions of others. These included Soviet researchers and their findings. Wiener's acquaintance with them caused him to be regarded with suspicion during the "Cold War". He was a strong advocate of automation to improve the standard of living, and to end economic underdevelopment. His ideas became influential in India, whose government he advised during the 1950s.
Wiener declined an invitation to join the Manhattan Project. After the war, he became increasingly concerned with what he believed was political interference with scientific research, and the militarization of science. His article "A Scientist Rebels" for the January 1947 issue of The Atlantic Monthly[1] urged scientists to consider the ethical implications of their work. After the war, he refused to accept any government funding or to work on military projects. The way Wiener's beliefs concerning nuclear weapons and the Cold War contrasted with that of John von Neumann is the major theme ofJohn Von Neumann and Norbert Wiener Heims (1980).[2]
Awards and honors
- Wiener won the Bôcher Prize during 1933 and the National Medal of Science during 1963 (Presented by President Johnson at a White House Ceremony during January 1964.), soon before his death.
- The Norbert Wiener Prize in Applied Mathematics was endowed during 1967 in honor of Norbert Wiener by MIT's mathematics department and is provided jointly by the American Mathematical Society and Society for Industrial and Applied Mathematics.
- The Norbert Wiener Award for Social and Professional Responsibility awarded annually by CPSR, was established during 1987 in honor of Wiener to recognize contributions by computer professionals to socially responsible use of computers.
- The crater Wiener on the far side of the Moon is named after him.
- The Norbert Wiener Center for Harmonic Analysis and Applications, at the University of Maryland, College Park, is named in his honor.[3]
- Robert A. Heinlein named a spaceship after him in his 1957 novel Citizen of the Galaxy; a 'Free Trader' ship called the Norbert Wiener mentioned in Chapter 14.
Work
Information is information not matter or energy—Norbert Wiener, Cybernetics (1948, p. 155)
Wiener was an early studier of stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.
Wiener is regarded as the originator of cybernetics, a formalization of the notion of feedback, with many implications for engineering, systems control, computer science, biology, philosophy, and the organization of society.
Wiener's work with cybernetics influenced Gregory Bateson and Margaret Mead, and through them, Anthropology, Sociology, and Education.[4]
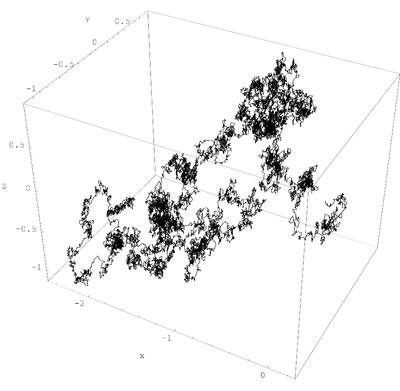
Wiener equation
A simple mathematical representation of Brownian motion, the Wiener equation, named after Wiener, assumes the current velocity of a fluid particle fluctuates.
Wiener filter
For signal processing, the Wiener filter is a filter proposed by Wiener during the 1940s and published during 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal.
In mathematics
The Wiener process is a continuous-time stochastic process named in honor of Wiener. It is often called Brownian motion', after Robert Brown. It is one of the best known Lévy processes, càdlàg stochastic processes with stationary statistical independence increments, and occurs frequently in pure and applied mathematics, economics and physics.
Wiener's tauberian theorem is a 1932 result of Wiener. It developed tauberian theorems in summability theory, on the face of it a chapter of real analysis, by showing that most of the known results could be encapsulated in a principle from harmonic analysis. As now formulated, the theorem of Wiener does not have any obvious association with tauberian theorems, which deal with infinite series; the translation from results formulated for integrals, or using the language of functional analysis and Banach algebras, is however a relatively routine process.
The Paley–Wiener theorem relates growth properties of entire functions on Cn and Fourier transformation of Schwartz distributions of compact support.
The Wiener–Khinchin theorem, also known as the Wiener – Khintchine theorem and sometimes as the Khinchin – Kolmogorov theorem, states that the power spectral density of a wide-sense-stationary random process is the Fourier transform of the corresponding autocorrelation function.
An abstract Wiener space is a mathematical object in measure theory, used to construct a "decent", strictly positive and locally finite measure on an infinite-dimensional vector space. Wiener's original construction only applied to the space of real-valued continuous paths on the unit interval, known as classical Wiener space. Leonard Gross provided the generalization to the case of a general separable Banach space.
The notion of a Banach space itself was discovered independently by both Wiener and Stefan Banach at around the same time.[5]
Publications
Wiener wrote many books and hundreds of articles:[6]
- 1914, "A simplification in the logic of relations" in Jean van Heijenoort, 1967. From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931. Harvard Univ. Press: 224-27.
- 1930, Extrapolation, Interpolation and Smoothing of Stationary Time Series with Engineering Applications. MIT Press. (Originally classified, finally published during 1949; the 1942 version of this monograph was nicknamed "the yellow peril" because of the color of the cover and the difficulty of the subject. [1])
- 1948, Cybernetics: Or Control and Communication in the Animal and the Machine. Paris, France: Librairie Hermann & Cie, and Cambridge, MA: MIT Press.Cambridge, MA: MIT Press. ISBN 9780262730099
- 1950, The Human Use of Human Beings. The Riverside Press (Houghton Mifflin Co.).
- 1958, Nonlinear Problems in Random Theory. MIT Press & Wiley.
- 1966, Generalized Harmonic Analysis and Tauberian Theorems. MIT Press.
- 1966, God & Golem, Inc.: A Comment on Certain Points Where Cybernetics Impinges on Religion. MIT Press.
- 1988, The Fourier Integral and Certain of its Applications (Cambridge Mathematical Library). Cambridge Univ. Press.
- 1994, Invention: The Care and Feeding of Ideas. MIT Press.
Fiction:
- 1959,The Tempter. Random House.
Autobiography:
- 1953. Ex-Prodigy: My Childhood and Youth. MIT Press.
- 1956. I am a Mathematician. MIT Press.
Under the name "W. Norbert"
- 1952 The Brain and other short science fiction in Tech Engineering News
References
- ↑ Norbert Wiener, "A Scientist Rebels," Atlantic Monthly, January, 1947, p. 46.
- ↑ John Von Neumann and Norbert Wiener: From Mathematics to the Technologies of Life and Death, MIT Press; 1980; ISBN 0262081059
- ↑ Norbert Wiener Center for Harmonic Analysis and Applications, University of Maryland, College Park
- ↑ Steve P. Heims, 1977: Gregory Bateson and the mathematicians: From interdisciplinary interaction to societal functions, Journal of the History of the Behavioral Sciences, Vol. 13. No. 2, pp. 141-159, Wiley Periodicals, Inc., A Wiley Company
- ↑ F. Albiac and N. Kalton, Topics in Banach Space Theory (GTM 233). New York: Springer 2006. p. 15
- ↑ A full bibliography is given by the Cybernetics Society Publications of Norbert Wiener
Further reading
- Bynum, Terrell W., "Norbert Wiener's Vision: The impact of "the automatic age" on our moral lives."
- Conway, F., and Siegelman, J., 2005. Dark Hero of the Information Age: in search of Norbert Wiener, the father of cybernetics. Basic Books, New York. 423pp. ISBN 0-7382-0368-8
- Montagnini, Leone, 2005. Le Armonie del disordine. Norbert Wiener Matematico-Filosofo del Novecento. Istituto Veneto di Scienze Lettere ed Arti, Venezia, 2005. XVI, 314 pp. ISBN 88-88143-41-6
- Ivor Grattan-Guinness, 2000. The Search for Mathematical Roots 1870-1940. Princeton Uni. Press.
- Bluma, Lars, 2005. Norbert Wiener und die Entstehung der Kybernetik im Zweiten Weltkrieg. Münster.
- Michel Faucheux, Nobert Wiener, le Golem et la cybernetique, Editions du Sandre,2008
- Heims, Steve J., 1980. John von Neumann and Norbert Wiener: From Mathematics to the Technologies of Life and Death. MIT Press.
- Heims, Steve J., 1993. Constructing a Social Science for Postwar America. The Cybernetics Group, 1946-1953. MIT Press.
- Ilgauds, Hans Joachim, 1980. Norbert Wiener.
- Masani, P. Rustom, 1990. Norbert Wiener 1894-1964. Birkhauser.
A brief profile of Dr. Wiener is given in The Observer newspaper, Sunday, 28 January 1951.
External links
- Norbert Wiener and Cybernetics – Living Internet
- O'Connor, John J.; Robertson, Edmund F., "Norbert Wiener", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Wiener_Norbert.html.
- Norbert Wiener at the Mathematics Genealogy Project
|
||||||||
|
||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||